Укажите номера прямоугольников, изображенных на рисунках 1−5, при вращении которых вокруг стороны AD получается цилиндр, осевым сечением которого является квадрат.
Запишите (11x)y в виде степени с основанием 11.
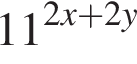
На рисунке изображен график движения автомобиля из пункта O в пункт N. Скорость движения автомобиля на участке MN (в км/ч) равна:
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно точки O.
Если 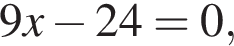 то
то 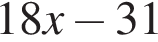 равно:
равно:
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что
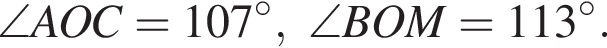 Найдите величину угла BOC.
Найдите величину угла BOC.
Решите неравенство 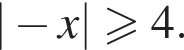
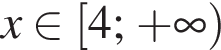
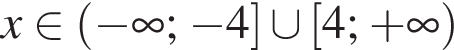
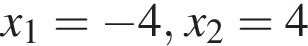

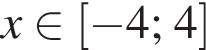
Даны числа: 45; 4,5 · 108; 0,045 · 106; 0,45; 45 · 103. Укажите число, записанное в стандартном виде.
В рамках акции «Книги — детям» школа получила некоторое количество книг, распределение которых по рубрикам показано на диаграмме: «І» — учебники и учебные пособия, «ІІ» — методические пособия, «ІІІ» — научно-популярная литература, «ІV» — художественная литература (см. рис.). Какое количество учебников и учебных пособий поступило в школу, если книг научно-популярной тематики и методических пособий было 396?
Найдите наименьший положительный корень уравнения 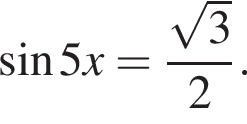
Упростите выражение 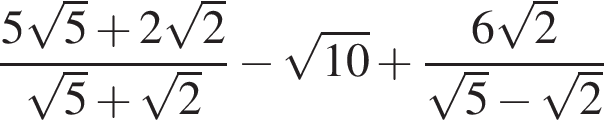
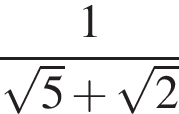
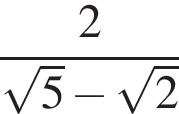
Свежие фрукты при сушке теряют a % своей массы. Укажите выражение, определяющее массу сухих фруктов (в килограммах), полученных из 35 кг свежих.
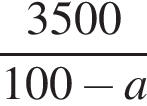
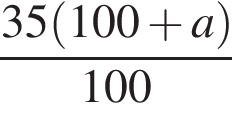
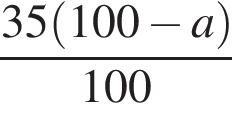
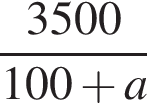
Параллельно стороне треугольника, равной 12, проведена прямая. Длина отрезка этой прямой, заключенного между сторонами треугольника, равна 8. Найдите отношение площади полученной трапеции к площади исходного треугольника.
Из пунктов A и B, расстояние между которыми 130 км, одновременно навстречу друг другу выехали два автомобиля с постоянными и неравными скоростями: из пункта A — со скоростью a км/ч, из пункта B — со скоростью b км/ч. Через некоторое время автомобили встретились. Составьте выражение, определяющее расстояние (в километрах) от пункта B до места встречи автомобилей.
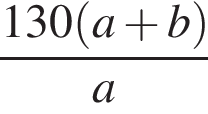
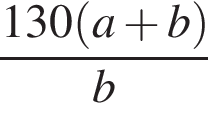
Точки A, B, C лежат на большой окружности сферы так, что треугольник ABC — равносторонний. Если AB = ![]() то площадь сферы равна:
то площадь сферы равна:
Найдите сумму наименьшего и наибольшего целых решений двойного неравенства 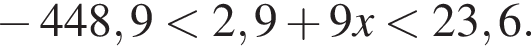
График функции, заданной формулой y = kx + b, симметричен относительно оси Oy и проходит через точку A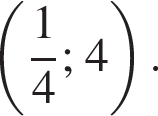 Значение выражения k + b равно:
Значение выражения k + b равно:
Корень уравнения
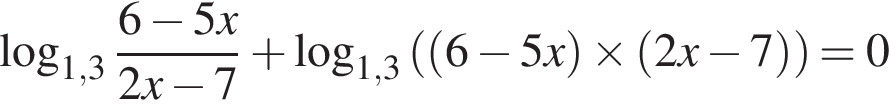
(или сумма корней, если их несколько) принадлежит промежутку:
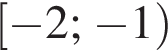
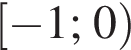
Найдите произведение корней уравнения 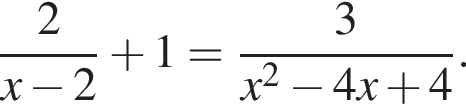
Найдите сумму корней (корень, если он единственный) уравнения 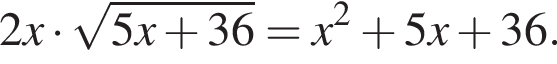
Известно, что при a, равном −2 и 4, значение выражения 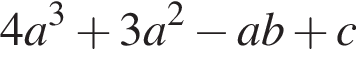 равно нулю. Найдите значение выражения b + с.
равно нулю. Найдите значение выражения b + с.
Пусть (x;y) — целочисленное решение системы уравнений
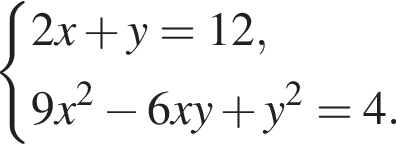
Найдите сумму x+y.
Найдите значение выражения 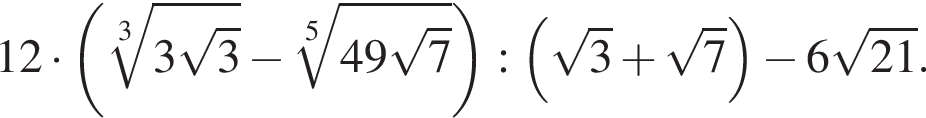
Найдите сумму корней уравнения 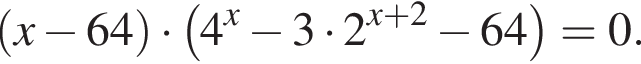
Четырёхугольник ABCD вписан в окружность. Если 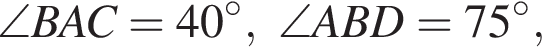 то градусная мера между прямыми AB и CD равна ...
то градусная мера между прямыми AB и CD равна ...
Найдите сумму корней уравнения
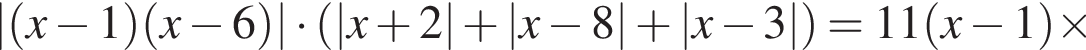
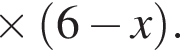
В арифметической прогрессии 120 членов, их сумма равна 120, а сумма членов с четными номерами на 360 больше суммы членов с нечетными номерами. Найдите пятидесятый член этой прогрессии.
Куб вписан в правильную четырехугольную пирамиду так, что четыре его вершины находятся на боковых ребрах пирамиды, а четыре другие вершины — на ее основании. Длина стороны основания пирамиды равна 4, высота пирамиды — 2. Найдите площадь S поверхности куба. В ответ запишите значение выражения 3S.
Количество целых решений неравенства 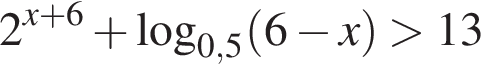 равно ...
равно ...
Трое рабочих (не все одинаковой квалификации) выполнили некоторую работу, работая поочередно. Сначала первый из них проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал
часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал
часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 6.
часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 6.

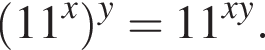
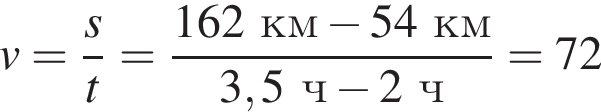 км/ч.
км/ч.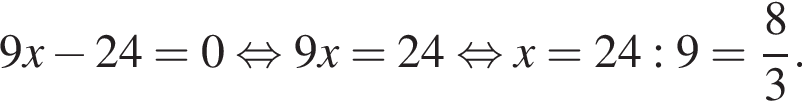
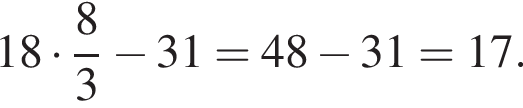
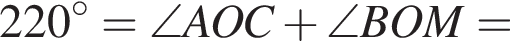

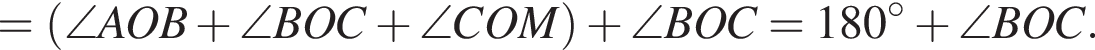




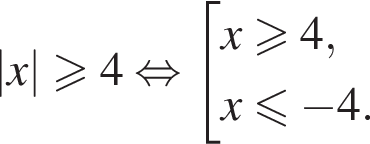
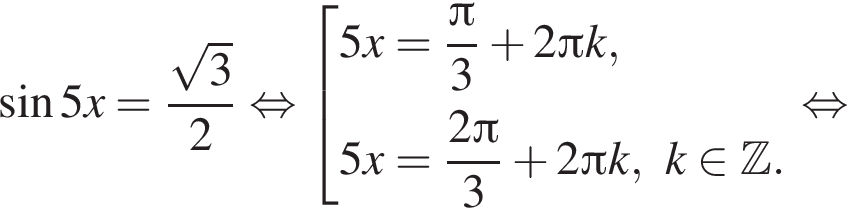
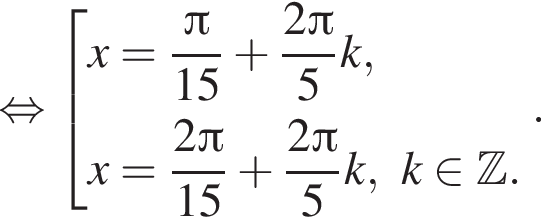
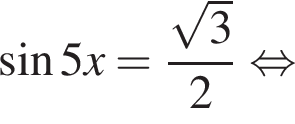
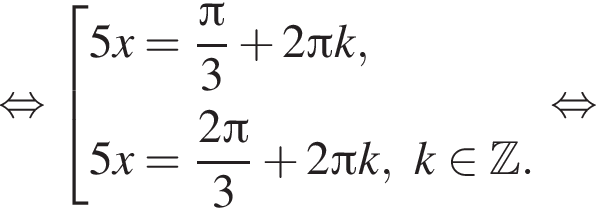
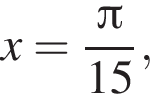 во второй —
во второй — 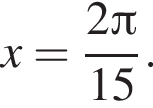 Таким образом, наименьший корень уравнения равен
Таким образом, наименьший корень уравнения равен 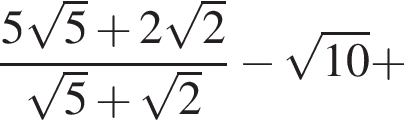
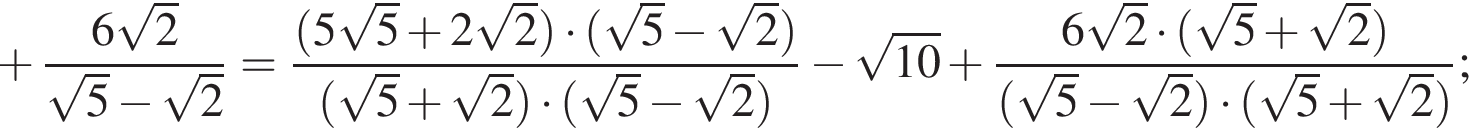
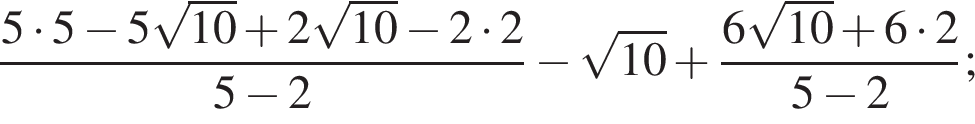
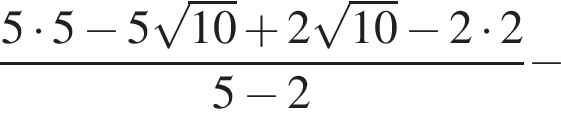
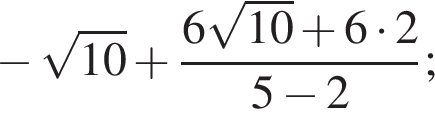
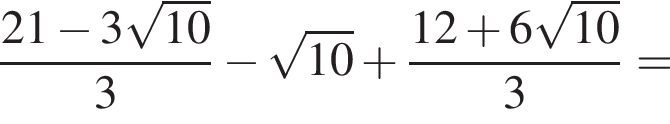
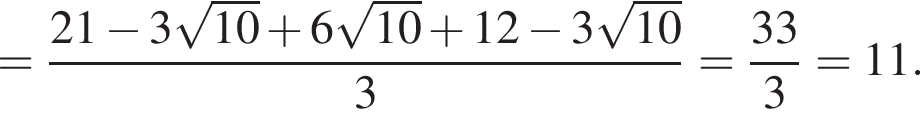
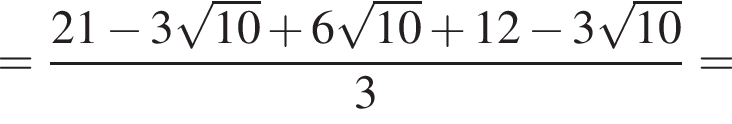
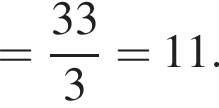
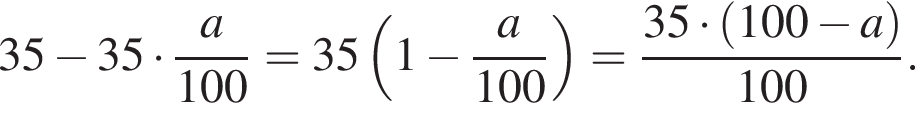
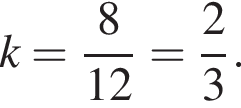 Площади подобных фигур относятся как квадрат коэффициента подобия. Поэтому
Площади подобных фигур относятся как квадрат коэффициента подобия. Поэтому 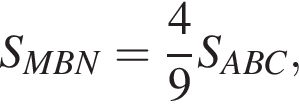 а тогда
а тогда 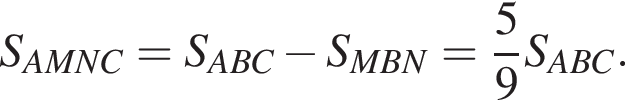
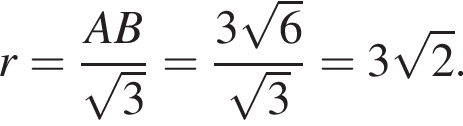 Площадь сферы равна
Площадь сферы равна 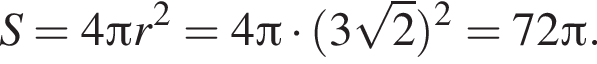
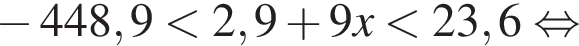
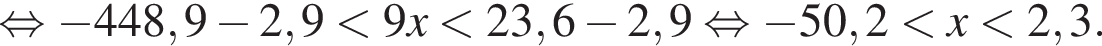

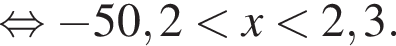
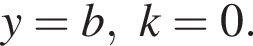 Прямая проходит через точку A с координатами
Прямая проходит через точку A с координатами 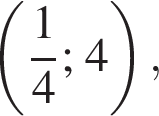 отсюда b = 4. Поэтому k + b = 4.
отсюда b = 4. Поэтому k + b = 4.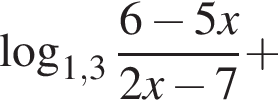
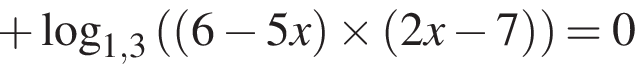
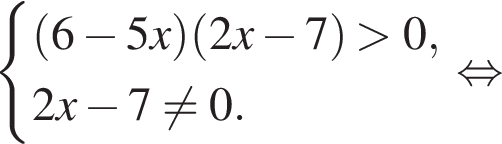
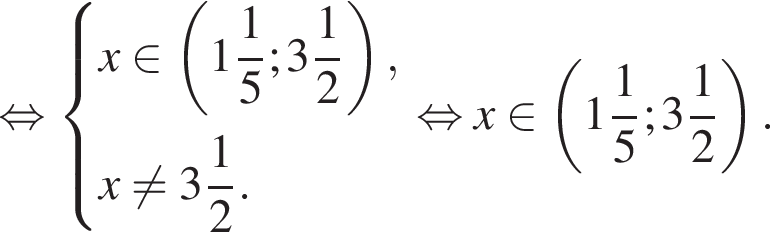
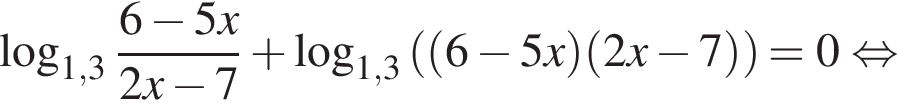
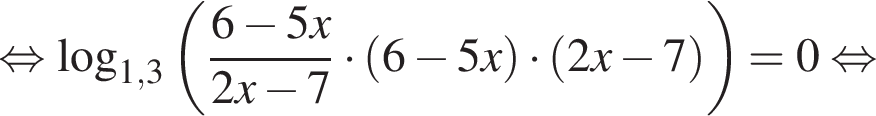
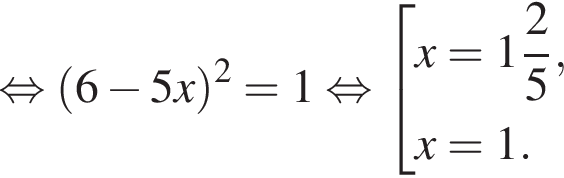
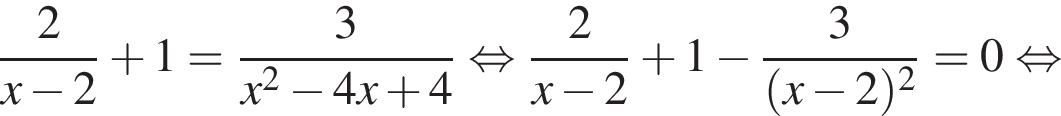
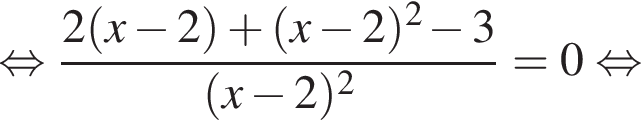
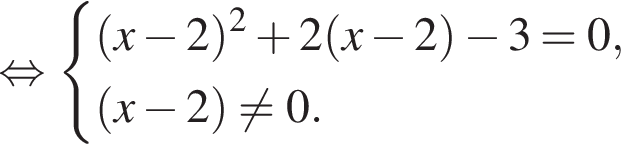
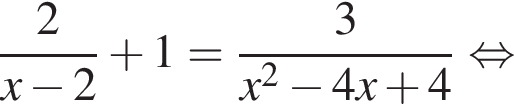
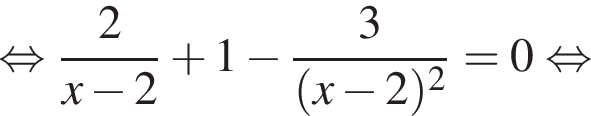
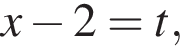 тогда:
тогда: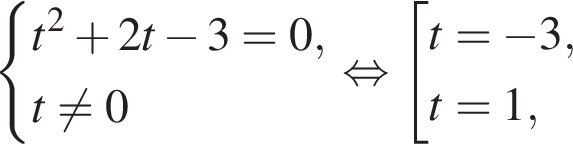
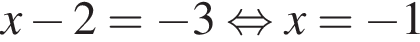 или
или 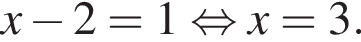
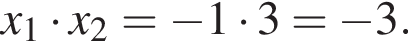
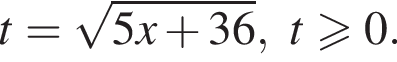 Тогда:
Тогда: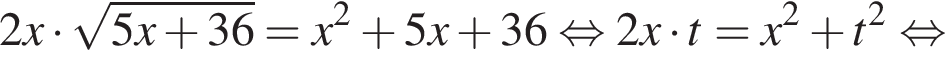

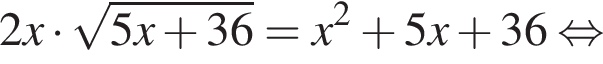


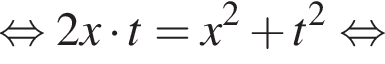
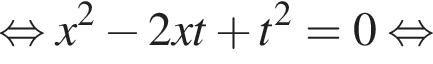
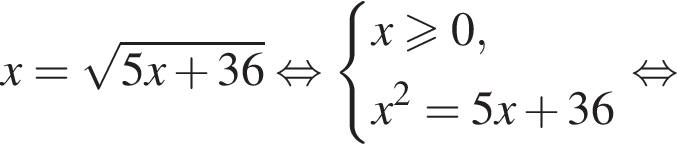
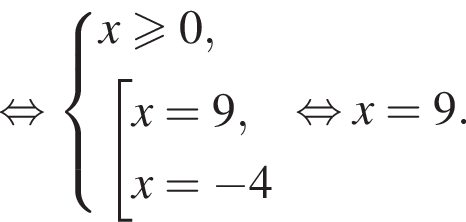
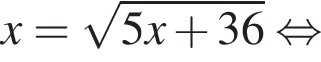
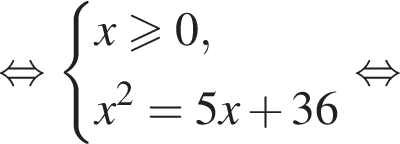
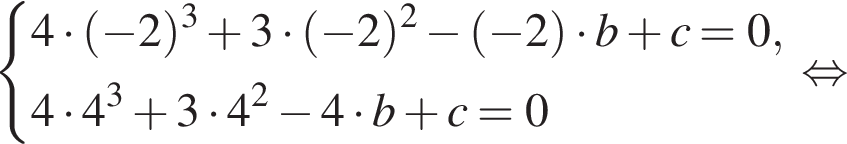
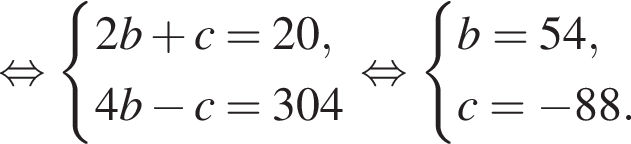
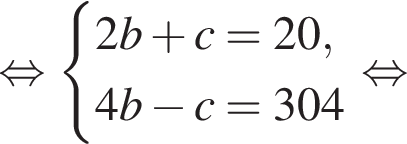
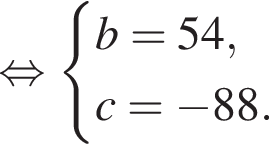

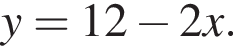 Заметим, что
Заметим, что 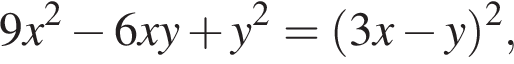 поэтому, подставляя y во второе уравнение системы получим:
поэтому, подставляя y во второе уравнение системы получим: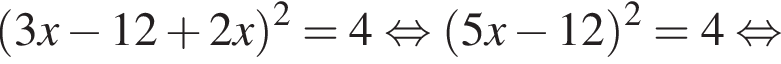
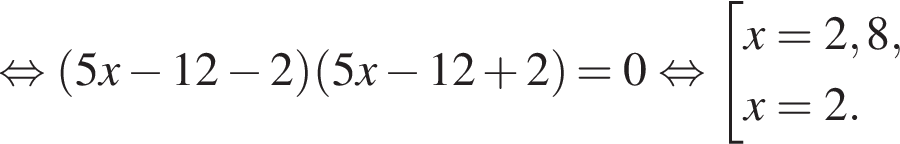
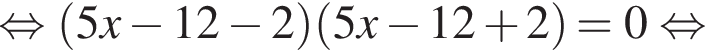
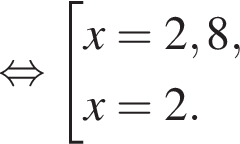
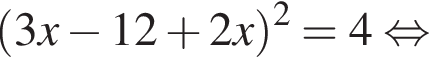
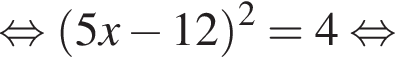
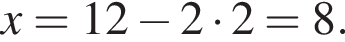 Сумма x+y равна:
Сумма x+y равна: 
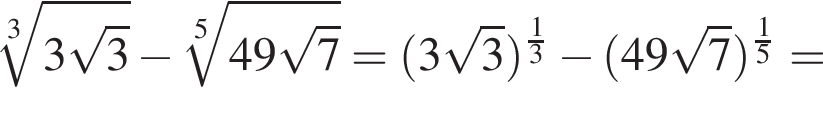
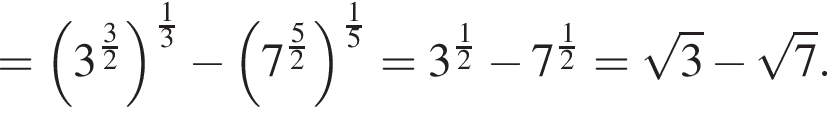
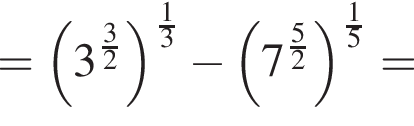
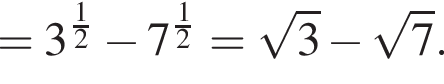
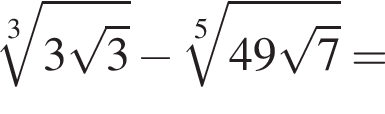
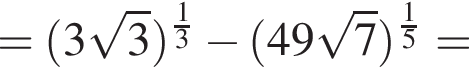
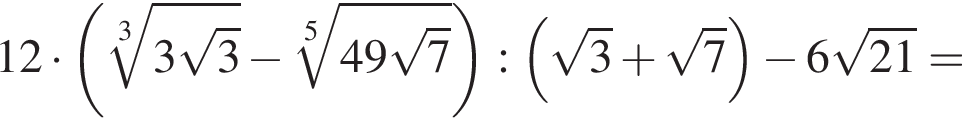
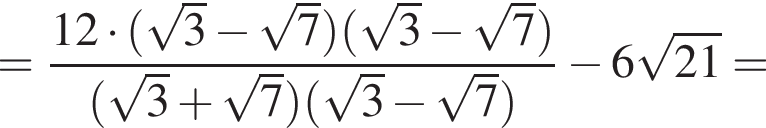
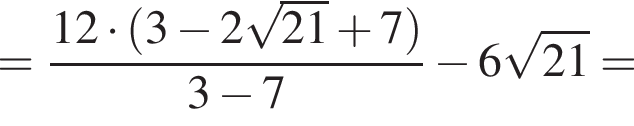
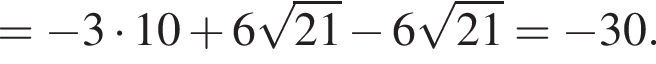

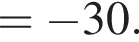
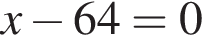 следует, что первый корень
следует, что первый корень  Рассмотрим
Рассмотрим 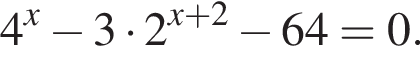 Сделаем замену
Сделаем замену 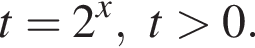 Тогда:
Тогда: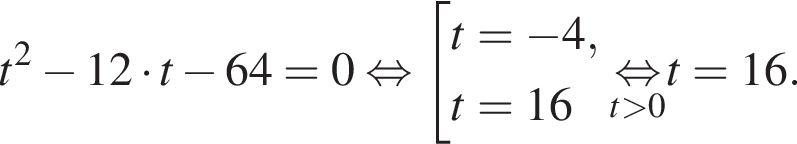
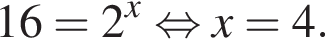 Отсюда следует, что сумма корней уравнения равна 68.
Отсюда следует, что сумма корней уравнения равна 68.

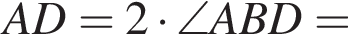

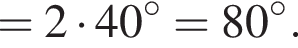
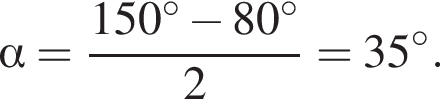

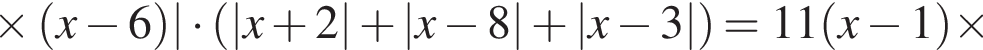
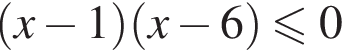 :
: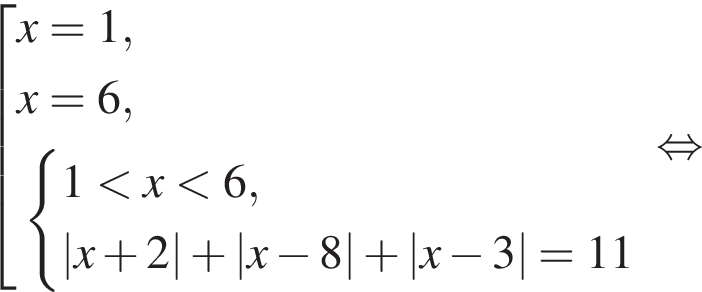
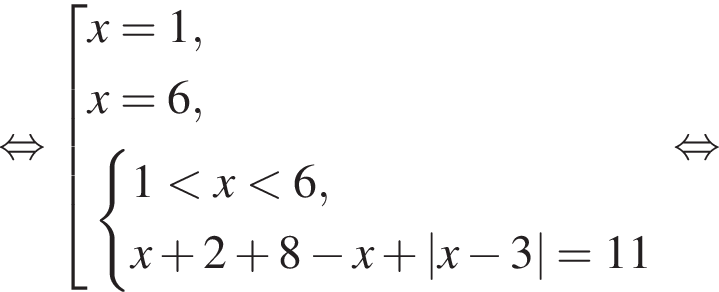
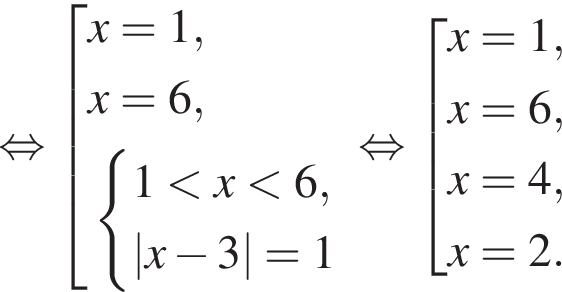
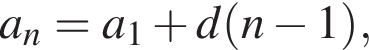 где d — разность арифметической прогрессии.
где d — разность арифметической прогрессии. 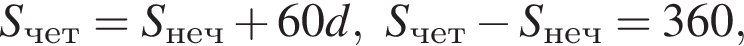 откуда
откуда 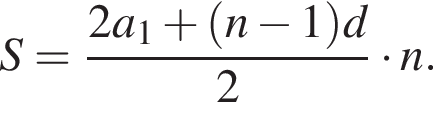 Следовательно, согласно условию, имеем:
Следовательно, согласно условию, имеем: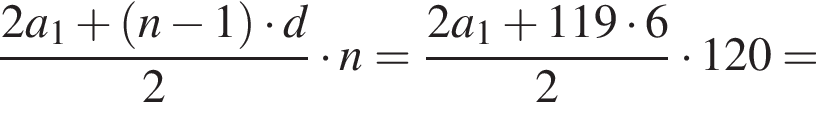
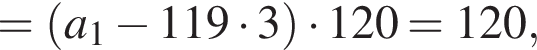
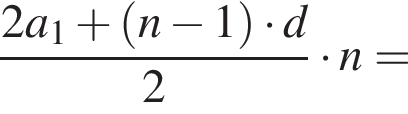
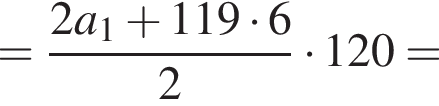
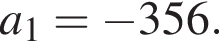 Получим
Получим 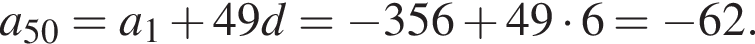
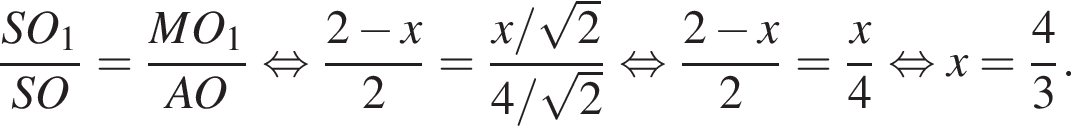
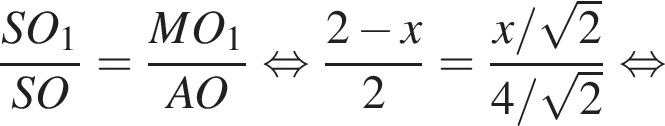
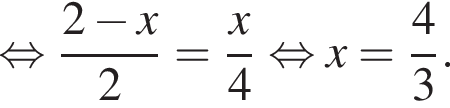
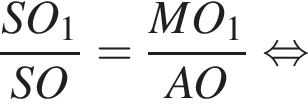
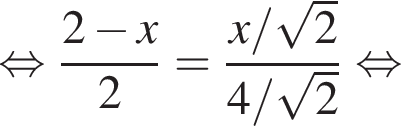
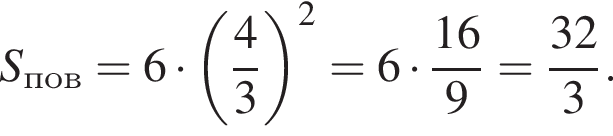
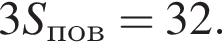
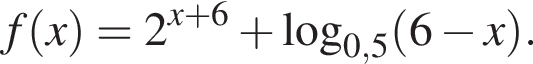 Заметим, что по смыслу задачи
Заметим, что по смыслу задачи 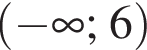
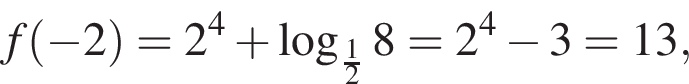 неравенство верно для всех x из
неравенство верно для всех x из 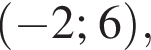 который содержит 7 целых чисел:
который содержит 7 целых чисел: 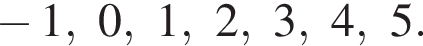
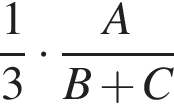 работы.
работы. 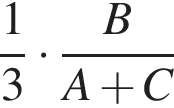 работы.
работы. 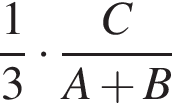 работы.
работы. 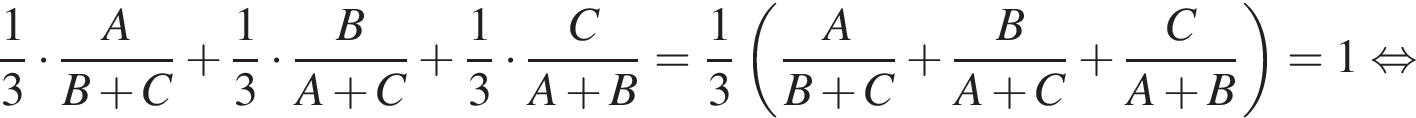
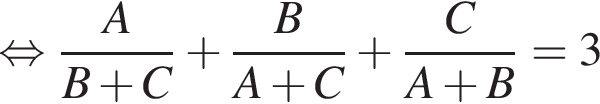
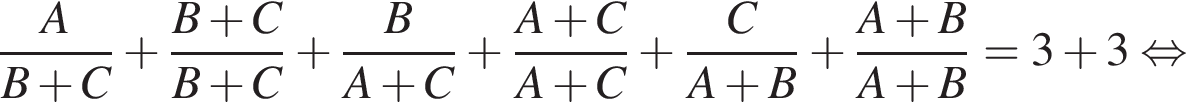
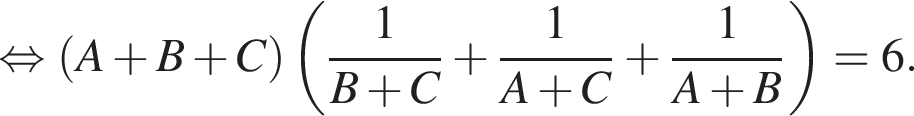
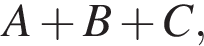 то они выполнили бы работу за:
то они выполнили бы работу за: 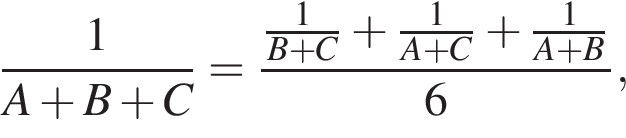
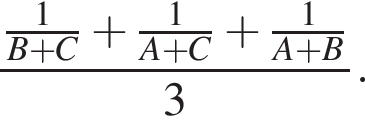 Поэтому, работая вместе работа была бы выполнена в
Поэтому, работая вместе работа была бы выполнена в 